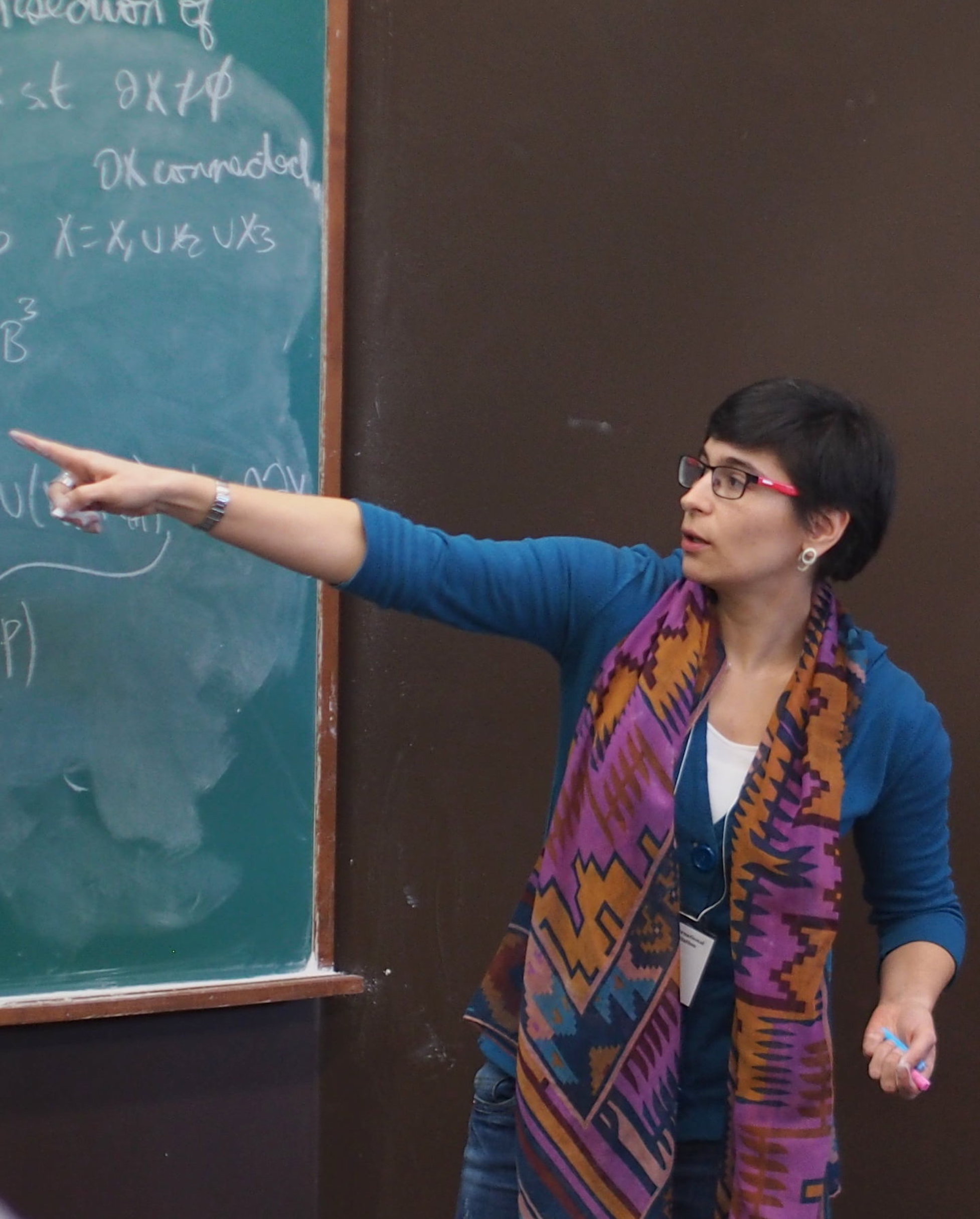| E-mail: | jpinzon@ncsu.edu | Office: | SAS Hall 3110 |
| Phone: | 919-513-2302 | Languages: | English, Spanish |
EDUCATION
-
2008-2014
Indiana University, Bloomington
PhD in Mathematics
Thesis: Independence of satellite operations of torus knots in the smooth concordance group.
Adviser: Paul Kirk.
-
2003-2007
Universidad de Los Andes
BSc in Mathematics
Thesis: Morse Homology.
Adviser: Bernardo Uribe.
Employment
-
2017-Today
NC State UniversityPostdoctoral Research Scholar
Mentors: Radmila Sazdanovic and Tye Lidman.
-
2014-2017
University of Georgia AthensPostdoctoral Teaching and Research Assistant
Mentor: David Gay.
Grants, Honors and Awards
- AIM SQuaRE - Trisections, Knotted Surfaces, and Symplectic 4-Manifolds, 2017
- NSF FRG Trisections - New Directions in Low-dimensional Topology, 2016
- OVPR Foreign Travel Assistance Program, University of Georgia 2015
- Provost’s Travel Award for Women in Science, Indiana University 2013
- David A. Rothrock Associate Instructor Award, Indiana University 2012
- Women in Science Program Travel Award, Indiana University 2012
- Women in Science Program Travel Award, Indiana University 2011
- Office of Women’s Affairs Fellowship, Indiana University 2008
- Teaching Assistanship, Universidad de Los Andes 2007
- Academic Excellence, Gimnasio Los Portales 2002
My research investigates the interplay between gauge-theoretic invariants and topological constructions. On the constructive side, my most current efforts have been concentrated around the development of the theory of trisections for 4–manifolds with boundary and of embedded surfaces in B^4. On the gauge- theoretical side, I have mostly studied the instanton moduli space. More details about my research can be found on my Research Statement.
PUBLICATIONS
Click here to find me on the arXiv.
Click here to find me on MathSciNet (subscription required.)
-
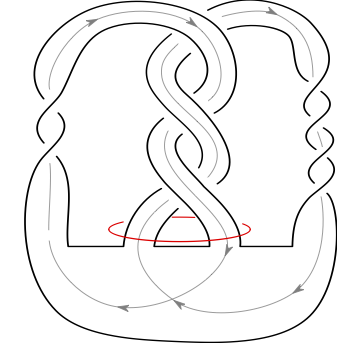
Satellites of Infinite Rank in the Smooth Concordance Group
Matthew Hedden, Juanita Pinzon-Caicedo
We conjecture that satellite operations are either constant or have infinite rank in the concordance group. We reduce this to the difficult case of winding number zero satellites, and use $SO(3)$ gauge theory to provide a general criterion sufficient for the image of a satellite operation to generate an infinite rank subgroup of the smooth concordance group $\mathcal{C}$. Our criterion applies widely, notably to scores of unknotted patterns for which the corresponding operators on the topological concordance group are zero. We raise some questions and conjectures regarding satellite operators and their interaction with concordance.
-
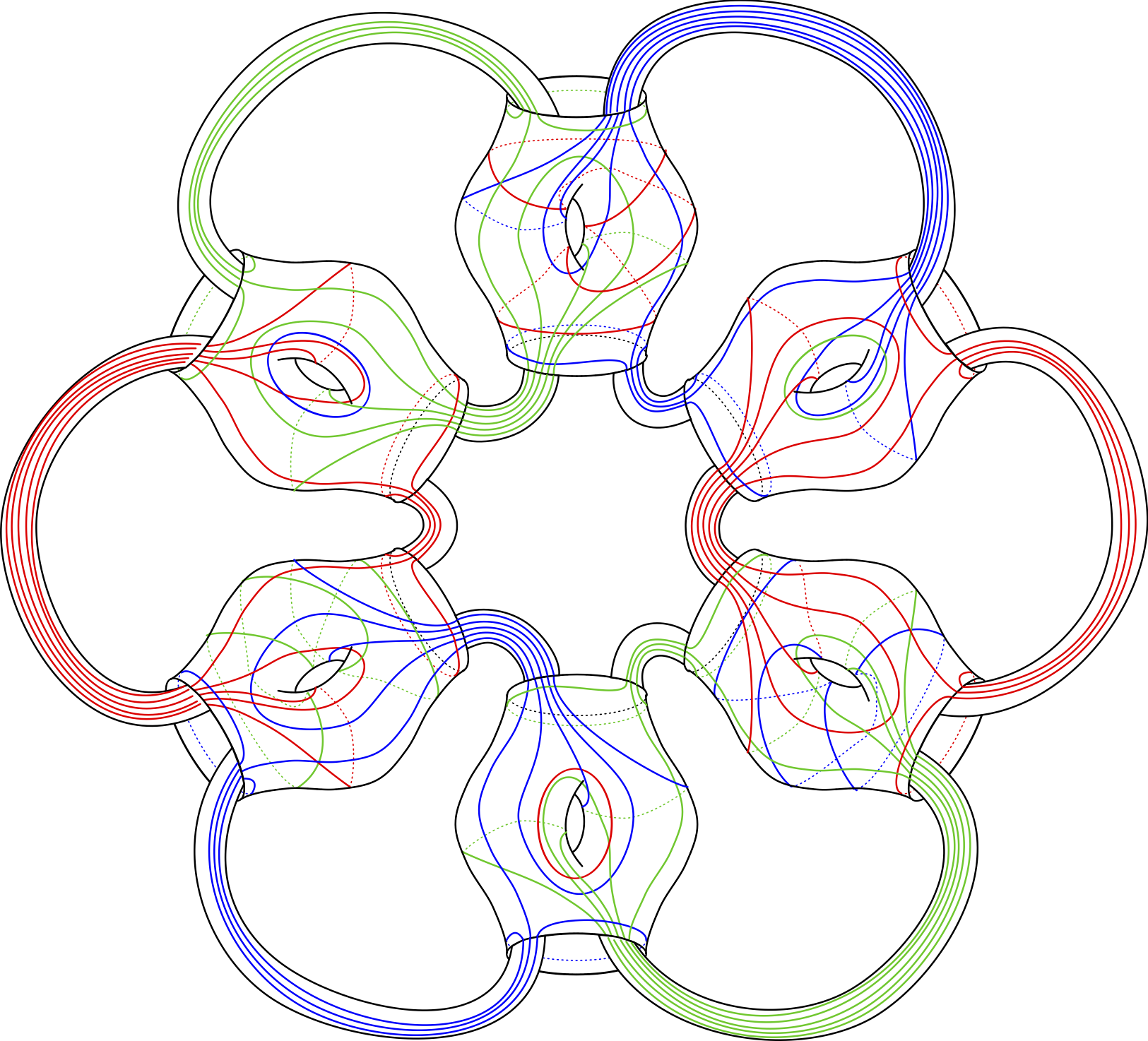
Trisections of 4-manifolds with Boundary
Nickolas A. Castro, David T. Gay, Juanita Pinzon-Caicedo
Given a handle decomposition of a 4-manifold with boundary, and an open book decomposition of the boundary, we show how to produce a trisection diagram of a trisection of the 4-manifold inducing the given open book. We do this by making the original proof of the existence of relative trisections more explicit, in terms of handles. Furthermore, we extend this existence result to the case of 4-manifolds with multiple boundary components, and show how trisected 4-manifolds with multiple boundary components glue together.
-
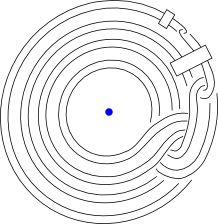
Independence of Iterated Whitehead Doubles
Juanita Pinzon-Caicedo
A theorem of Furuta and Fintushel-Stern provides a criterion for a collection of Seifert fibred homology spheres to be independent in the homology cobordism group of oriented homology 3-spheres. In this article we use these results and some 4-dimensional constructions to produce infinite families of positive torus knots whose iterated Whitehead doubles are independent in the smooth concordance group.
-
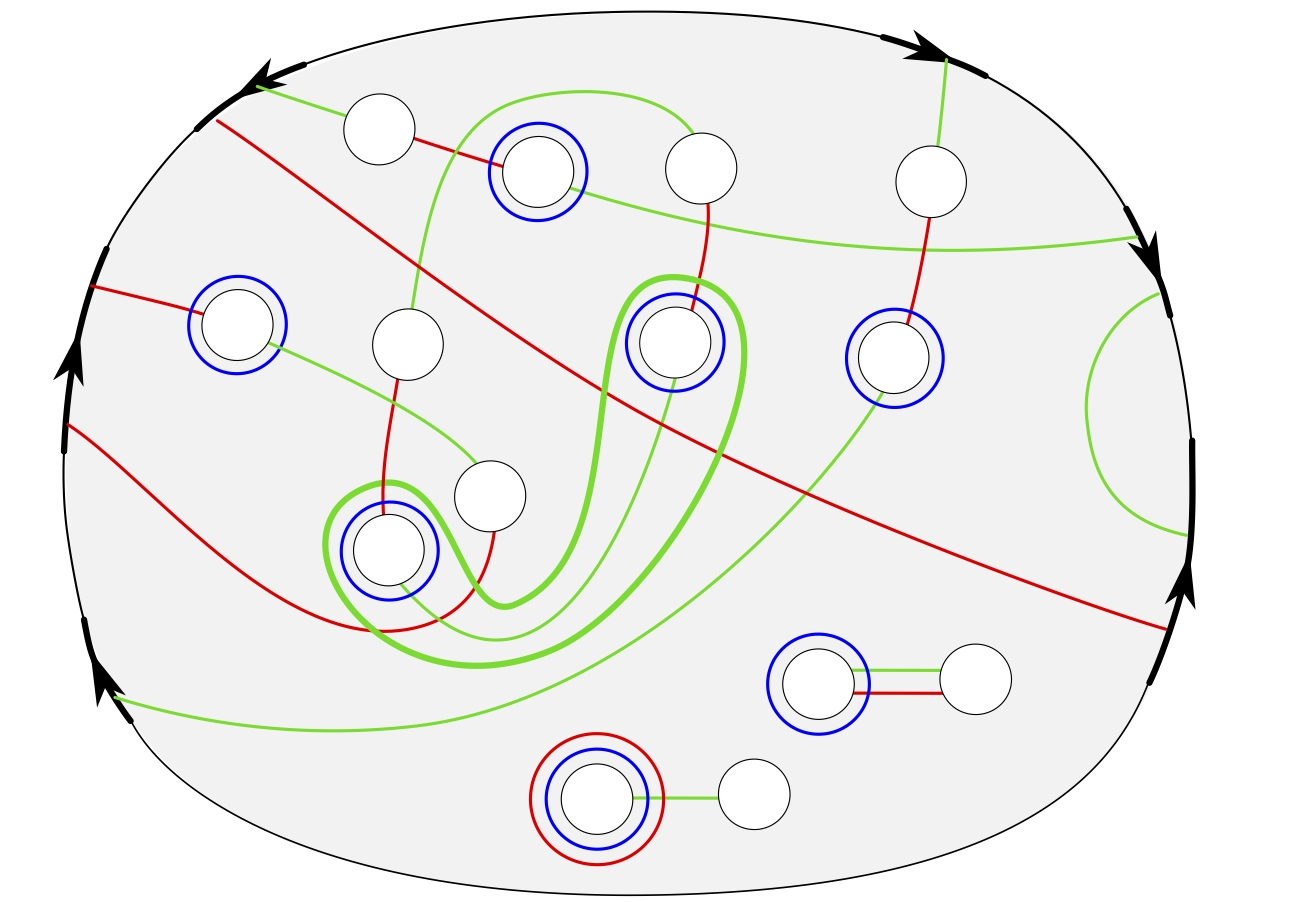
Diagrams for Relative Trisections
Nickolas A. Castro, David T. Gay, Juanita Pinzon-Caicedo
We establish a correspondence between trisections of smooth, compact, oriented 4--manifolds with connected boundary and diagrams describing these trisected 4--manifolds. Such a diagram comes in the form of a compact, oriented surface with boundary together with three tuples of simple closed curves, with possibly fewer curves than the genus of the surface, satisfying a pairwise standardness condition. This should be thought of as the 4--dimensional analog of a sutured Heegaard diagram for a sutured 3--manifold. We also give many foundational examples.
-
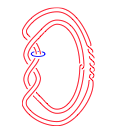
Independence of Satellites of Torus Knots in the Smooth Concordance Group
Juanita Pinzon-Caicedo
The main goal of this article is to obtain a condition under which an infinite collection ℱ of satellite knots (with companion a positive torus knot and pattern similar to the Whitehead link) freely generates a subgroup of infinite rank in the smooth concordance group. This goal is attained by examining both the instanton moduli space over a 4-manifold with tubular ends and the corresponding Chern-Simons invariant of the adequate 3-dimensional portion of the 4-manifold. More specifically, the result is derived from Furuta's criterion for the independence of Seifert fibred homology spheres in the homology cobordism group of oriented homology 3-spheres. Indeed, we first associate to ℱ the corresponding collection of 2-fold covers of the 3-sphere branched over the elements of ℱ and then introduce definite cobordisms from the aforementioned covers of the satellites to a number of Seifert fibered homology spheres. This allows us to apply Furuta's criterion and thus obtain a condition that guarantees the independence of the family ℱ in the smooth concordance group.
-
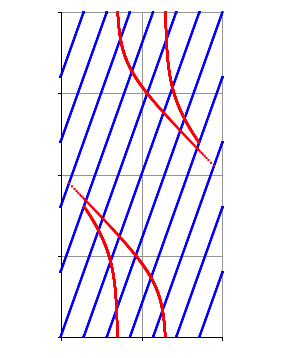
Traceless SU(2) representations of 2-stranded tangles
Yoshihiro Fukumoto, Paul Kirk, Juanita Pinzon-Caicedo
Given a 2-stranded tangle T contained in a ℤ-homology ball Y, we investigate the character variety R(Y,T) of conjugacy classes of traceless SU(2) representations of π1(Y \ T). In particular we completely determine the subspace of binary dihedral representations, and identify all of R(Y, T) for many tangles naturally associated to knots in S 3. Moreover, we determine the image of the restriction map from R(T, Y) to the traceless SU(2) character variety of the 4-punctured 2-sphere (the pillowcase). We give examples to show this image can be non-linear in general, and show it is linear for tangles associated to pretzel knots.
SELECTED TALKS
-

Gauge Theory and Knot Concordance
Latinx in Math, Duke Topology Seminar, MSU Topology Seminar
Knot concordance can be regarded as the study of knots as boundaries of surfaces embedded in spaces of dimension 4. Specifically, two knots K0 and K1 are said to be smoothly concordant if there is a smooth embedding of the 2—dimensional annulus S1 × [0, 1] into the 4—dimensional cylinder S3 × [0, 1] that restricts to the given knots at each end. Smooth concordance is an equivalence relation, and the set of smooth concordance classes of knots, C, is an abelian group with connected sum as the binary operation. The algebraic structure of C, the concordance class of the unknot, and the set of knots that are topologically slice but not smoothly slice are much studied objects in low-dimensional topology. Gauge theoretical results on the nonexistence of certain definite smooth 4-manifolds can be used to better understand these objects. In particular, the study of anti-self dual connections on 4-manifolds can be used to shown that (1) the group of topologically slice knots up to smooth concordance contains a subgroup isomorphic to Z^\infty, and (2) satellite operations that are similar to cables are not homomorphisms on C.
Poster -

La dimensión 4 y la concordancia de nudos
XXI Congreso Colombiano de Matematicas
La meta principal de la topología geométrica es la clasificación de las variedades según su estructura (topológica, suave, simpléctica, etc.). En dimensión 4 la historia es especial: es la única dimensión en la que una variedad puede admitir un número infinito de estructuras suaves no equivalentes y la única dimensión en la que existen variedades homeomorfas pero no difeomorfas a R^4. A su vez, la concordancia de nudos es el estudio de los nudos como fronteras de superficies encajadas en espacios de dimensión 4. La diferencia entre estructuras topológicas y estructuras suaves en dimensión 4 está estrechamente relacionada con la concordancia de nudos. En la charla explicaré una faceta de ésta relación.
-

Examples of relative trisections
AMS Sectional NCSU, Georgia Tech, AMS Sectional St. Thomas University, HIM
Trisections of 4-manifolds relative to their boundary were introduced by Gay and Kirby in 2012. They are decompositions of 4-manifolds that induce open book decomposition in the bounding 3-manifolds. This talk will focus on diagrams of relative trisections and will be divided in two. In the first half I will focus on trisections as fillings of open book decompositions and I will present different fillings of different open book decompositions of the Poincare homology sphere. In the second half I will show examples of trisections of pieces of some of the surgery techniques that result in exotic 4-manifolds.
Slides1 Slides2 -
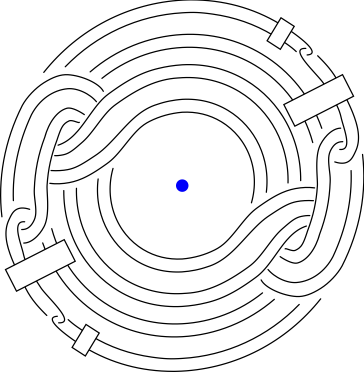
Iterated Whitehead Doubles are Independent
MPIM
In the 1980’s Furuta and Fintushel-Stern applied the theory of instantons and Chern-Simons invariants to develop a criterion for a collection of Seifert fibred homology spheres to be independent in the homology cobordism group of oriented homology 3-spheres. These results, together with some 4-dimensional constructions can be used to show that iterated Whitehead doubles of positive torus knots are independent in the smooth concordance group.
-
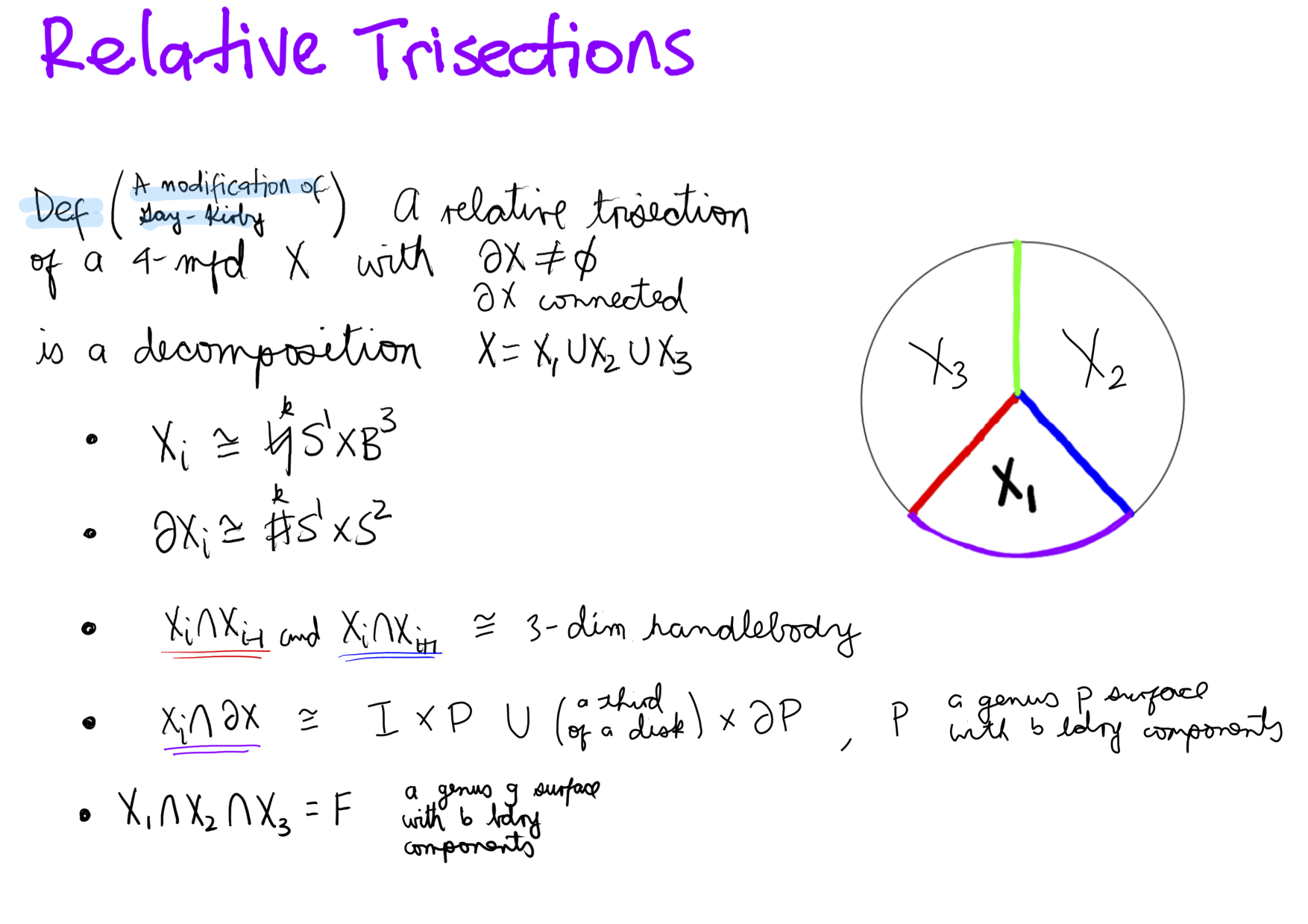
An Overview of Relative Trisections
University of Iowa, AMS Sectional UGA, BIRS, SUNY Buffalo
Based on the notion of trisections of closed 4--manifolds of Gay and Kirby, Nick Castro and myself developed a rigorous definition of relative trisections as a generalization of trisections to 4--manifolds with boundary. In the talk I will present the basics of relative trisections starting with their relationship to open book decompositions of the bounding manifolds. I will then introduce a stabilization operation that gives rise to a statement about the uniqueness of relative trisections, thus complementing Gay and Kirby's proof of the existence of relative trisections. Finally, I will introduce the notion of diagrams of relative trisections and describe a method to recover the open book decomposition of the bounding manifold from the trisection diagrams.
Slides Video -

Construcciones de 3-variedades y la esfera de Poincaré
Matemáticas por estudiantes, Universidad de Los Andes
En 1910 Henri Poincare publicó un articulo en el que afirmaba que los grupos de homología eran suficientes para determinar si una 3-variedad es la 3-esfera S3. Cuatro años más adelante Poincaré mismo publicó la descripción de una 3-variedad con los mismos grupos de homología que S3 pero distinta a esta última. Hoy en día este espacio se conoce como la esfera de Poincaré y parte de su encanto radica en que se puede describir de distintas maneras, todas construcciones de enorme importancia en el estudio de 3-variedades. La idea de la charla es describir algunas de estas construcciones a través de la esfera de Poincaré. Algunas de las construcciones que intentaré describir son cirugía de Dehn, espacios recubridores ramificados y espacios cocientes.
-
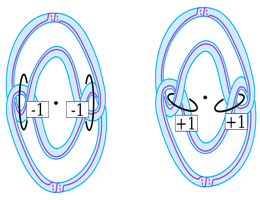
Independence of Whitehead Doubles of Torus Knots in the Smooth Concordance Group
Georgia Tech, Brandeis University, Knots in the Triangle, University of Georgia, IAS, University of Minnesota
In the 1980’s Furuta and Fintushel-Stern applied the theory of instantons and Chern-Simons invariants to develop a criterion for a collection of special homology spheres to be independent in the homology cobordism group of oriented homology 3-spheres. Hedden and Kirk then use the aforementioned criterion to establish conditions under which an infinite family of Whitehead doubles of positive torus knots are independent in the smooth concordance group. In the talk, I will review some of the definitions and constructions involved in the proof by Hedden and Kirk and I will introduce some topological constructions that simplify and extend their argument.
Slides -

3-Esferas de Homología
Oaxaca
Una 3-esfera de homología es una variedad diferencial cerrada y orientada que tiene mismos grupos de homología de la 3-esfera. En el mini-curso presentaré diferentes construcciones de este tipo de objetos, introduciré los invariantes de Rokhlin y Casson para finalmente hablar de la estructura algebraica del grupo de cobordismo de 3-esferas de homología.
-
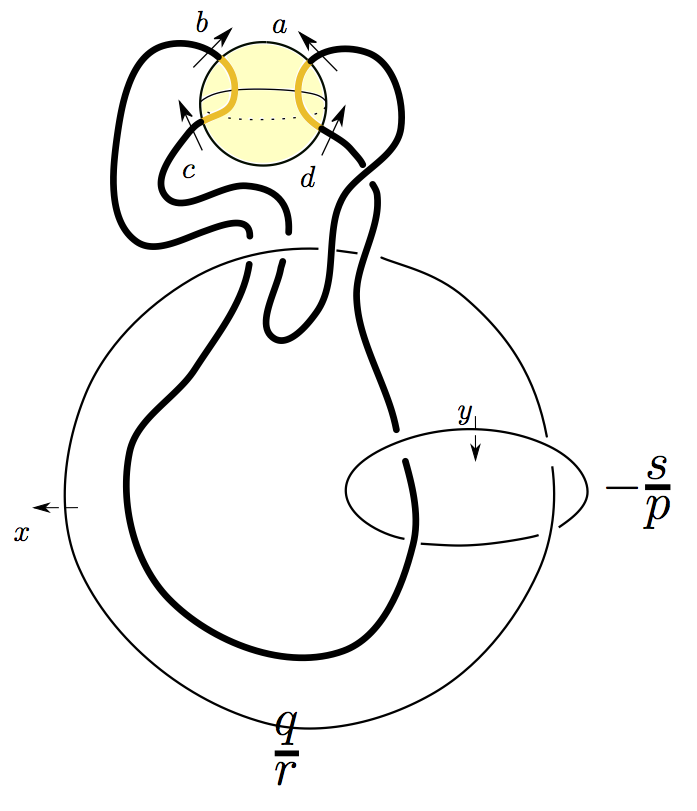
Traceless SU(2) representations of 2-stranded tangles
Michigan State, Louisiana State University
Given a codimension 2 submanifold A⊂X define R(X,A) as the space of traceless SU(2) representations of π_1(X\A) modulo conjugation. For Y a 3-manifold and K⊂Y a knot, Kronheimer-Mrowka defined the Instanton Knot Homology of (Y,K) as the homology of a chain complex whose groups are generated by the elements of R(Y,K). In the talk we describe a method to determine R(S^3,K) whenever K is a torus or pretzel knot.
Slides
I find the most effective way to impart knowledge is through dialogue: I view teaching as a circle of communication between the students and myself, and in my classroom I work for this mutual interaction. In practice, this means that I direct the discussion toward exploration of concepts and propose pertinent questions that prompt the students to be active participants. By building upon class participation and mutual interaction I work to turn students into active agents, going from passively receiving knowledge to generating it.
20+
Classes
10+ years
Teaching Experience
900+
Students
Teaching Experience
-
Mathematics Courses
Courses typically taken by math majors or graduate students in mathematics.- Vector Bundles and Characteristic Classes
PhD level course.
- Algebraic Topology
PhD level course. One semester as a teaching assistant.
- Point-set Topology
One semester as the main instructor. Mixed undergraduate/graduate course.
- Calculus on Manifolds
One semester experience as a teaching assistant.
- Vector Bundles and Characteristic Classes
-
Mathematics Requirement
Courses taken by non-math majors to fullfill a mathematics requirement.- Calculus
Six semesters as the main instructor, four semesters as an assistant. Class size 20-100.
- Pre-Calculus
Two semesters as the main instructor. About 30 students per class.
- Finite Mathematics
Four semesters as the main instructor, one semester as an assistant. Class size 20-200.
- Calculus
-
Mathematics Education
Content courses for students majoring in education.- Foundations of Geometry
One semester as the main instructor. Mixed undergraduate/graduate course.
- Modern Algebra for Secondary School Teachers
One semester experience as a teaching assistant.
- Topics in Euclidean Geometry
One semester experience as a teaching assistant.
- Foundations of Geometry